熱伝導方程式
微小区間における熱の出入りを考える。
熱の伝導を記述するのに必要な概念・法則等は大別すると、熱伝導率、フーリエの法則、熱容量の3つである。
1)
熱伝導率:
幅1[m]で隔てられた面積1[
]の二つの面に1[K]の温度差があるとき、微小時間
(=1[s])に流れる熱量
[J]を、
熱伝導率:（カイ）
と定義する。なお、[W]=[J/s]は仕事の単位である。
2)
フーリエの法則
厚さ
、面積
で囲われたある微小区間
[
]内の断面を通過する熱の総量は、熱伝導率、接触面積
、温度
、温度勾配
、微小時間に比例する。すなわち、
が成り立つ。
3)
熱容量:
ある物質の熱容量は、その物質の密度を
とすると、質量
および比熱
の積に比例する。すなわち、
この熱容量を持つ物質に熱量
を与えるとその物質の温度が
変化する。この物質に与えた熱量と温度変化の間には、熱容量を比例定数として、以下の関係が成立する。
以上の概念をベースにして、下図の中央の座標
における微小区間
についての熱の変化
を考える。
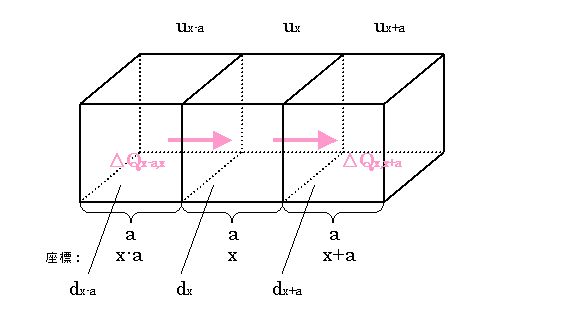
i) 熱の流出入による熱量の変化
上図において微小区間との温度差は、左側の微小区間
と、右側の微小区間
との間にのみある「一次元の温度勾配」とし、それぞれの温度は、
を満たすものとする（つまり左側のほうが温度が高い）。この場合、微小区間から微小区間に向かって熱量
が流れこみ、微小区間から微小区間に向かって熱量
が流れ出すことになる。それぞれの熱量はフーリエの法則を用いると、
、
となる。よって中央の微小区間における熱量の変化は、
となる。
ii)
熱容量と温度変化を考えた場合の熱量の変化
熱容量の関係から、
となる。
i)、ii)の結果から、
よって、
ただし、
は温度拡散率と呼ばれるものである。
ここで、
の極限を考えると、
よって、
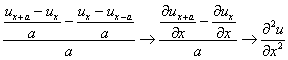
一方、
以上より、熱伝導方程式：
が導かれる。
例題１）有限の長さ1
をもつ棒に対する熱伝導方程式の一般解
を求め、その初期値境界値問題を解け。
解）変数分離法を利用し一般解を求め、フーリエ級数を用いて、初期値と境界条件から特解を決定する。
まず、変数分離法http://www.aksystem.jp/math/VariablesSeparation/VariablesSeparation.htmより、
とおく。これらの一般解はそれぞれ、
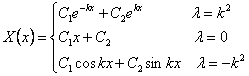
これを
について、場合分けして考える。
i)
の場合
となるので、
ただし、
であるが、境界条件より、
が必要。しかし、例えば、
となり、初期値が満たされない。よって、不適。
ii)
の場合
となるので、
ただし、
であるが、初期値と境界条件より、
よって、
が必要となるが、
であるためには、
が必要となり、これではやはり、
となってしまい、初期値が満たされない。よって、不適。
iii)
の場合
となるので、
ただし、
であるが、境界条件より、
より、
が必要。またもう一方の境界条件、
より、
もしくは 
のいずれかが必要。しかし、では、初期条件、
が満たされない。よって、のみが残された唯一の希望となる。この場合
は、
を満たす必要がある。これよりこの熱伝導方程式を満たすとして、
が求まり、これを固有値として、解はそれぞれの固有値に対して、
を満たすことが必要となることがわかった。さて、この中から初期条件を満たす特解を探し出すわけであるが、それぞれの
に対して、実は、
となってしまい、初期条件を満たさない。そこで、この解を無数に重ね合わせる（つまりフーリエ級数を形成する。これを重ね合わせ法と呼ぶ）と、
となり、これは与えられた熱伝導方程式を満たしていることがわかる。なぜならば、
となり、確かに、
となっている。よって、これは与えられた熱伝導方程式の一般解となる。
次に、この初期値を満たす解を探し出すことにしよう。初期値、
より、
となるが、これはフーリエ級数の係数を求める問題に他ならない。初期値の関数を
として、両辺に
をかけて0から1まで積分すると、
ここで、
とおくと、
となるので、
i)
のとき
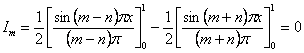
ii)
のとき
これより、
ただし、
はクロネッカーのデルタとよばれ、
を満たすものである。以上より、
となることがわかったので、これを実際に積分すると、
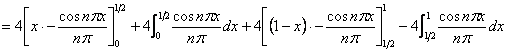
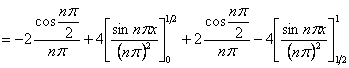
以上より特解は、
となる。
例題２）無限の長さを持つ棒
の熱伝導方程式の初期値問題を解け。
解）無限区間の熱伝導方程式なので、フーリエ変換を用いた解法を試みる。
とおく。例題１）と同様に、一般解はそれぞれ、
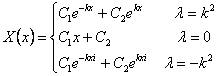
と求まる（注１）。これをについて、場合分けして考える。
注１）後の展開を考え、ここではあえて虚数解のままの形で残してある。
i)
の場合
となるので、
ただし、
であるが、この場合、
となり、初期条件が満たされない。よって、不適。
ii)
の場合
となるので、
ただし、
であるが、この場合、
となり、やはり初期条件が満たされない。（例えば
とすると一般解は発散するが、
のはず）よって、不適。
iii)
の場合
となるので、
ただし、
が必要となる。この場合、の値はまだ決めることが出来ないので、それぞれのに対する積分定数を
とすると、
とそれぞれの固有解を書くことが出来る。有限区間の場合に与えられていた境界条件は、本問では与えられていないので、具体的にが満たすべき条件を決定することは出来ない。そこで、をそのまま連続な変数と見なし、重ね合わせ法を拡張して、総和の代わりに
から
までの積分であらわすこととする。よって、
ここで、が連続で無数にあるので、あるとは符号が反対の
が必ず存在し、
があれば、
もまた存在するので、ここからそれぞれ、
と、
が選べるので、
とおけば、
と
を書き改めることが出来る。これは与えられた熱伝導方程式を満たしていることがわかる。なぜならば、
となり、確かに、
となっている。よって、与えられた熱伝導方程式の一般解：
を得た。
次に、この初期値を満たす解を探し出すことにしよう。初期値、
より、
となるが、第2項はよく見ると
のフーリエ逆変換に他ならない。よってそのフーリエ変換は、
一方、第3項においては
のフーリエ変換が、
であることを使うと（TODO: のフーリエ変換の説明）、それぞれのフーリエ変換が等しいことから、
となるので、
となる。両辺をで偏微分して、
これに部分積分を施して、
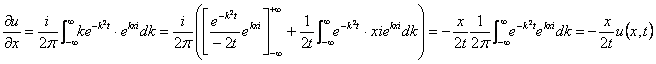
よって、この微分方程式を解くと、
＝＞ 
＝＞ 
よって、
に
を代入すると、
であるのだが、有名な公式、
を使えば、
となるので、
が求める特解である。
例題３）例題２）において、温度拡散率
と初期値が一般の関数
として与えられた場合に、特解の一般形を求めよ。
解）例題２と同様の方法でまず一般解を求める。
とおく。例題２）と同様に、一般解はそれぞれ、
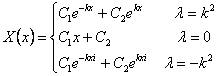
と求まる（注２）。これをについて、場合分けして考える。
注２）後の展開を考え、ここではあえて虚数解のままの形で残してある。
i)
の場合
例題２）の結果を用いて、
ただし、
となる場合に限り、適合。
ii)
の場合
例題２）の結果を用いて、
ただし、
となる場合に限り、適合。
iii)
の場合
例題２）の結果を用いて、
となっている。次に、この初期値を満たす解を探し出すことにしよう。初期値、
より、
となるが、これはのフーリエ逆変換に他ならない。よって、のフーリエ変換が、
であることを使い、上の式にフーリエ変換を施すと、
となるので、
となる。ここで、この式を変形し、
として、その一部を、
とおこう。
の両辺をで偏微分して、
これにの部分積分を施して、
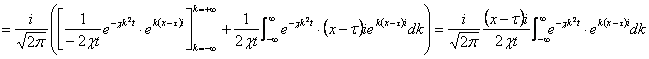
よって、
この偏微分方程式を解くと、
＝＞ 
＝＞ 
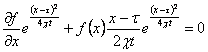よって、
にを代入すると、
となるがこの式にオイラーの公式を適用すると、
となり、
と
が遇関数、
が奇関数であることを考慮すると、
となる。ここで、
とおいて、
で偏微分すると、
これにの部分積分を施すと、
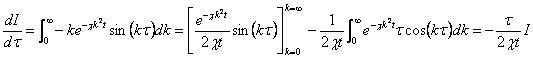
となるので、この微分方程式を解くと、
＝＞ 
＝＞ 
＝＞ 
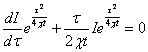よって、
となるが、
となるので、有名な公式、
を使えば、
となるので、
これを、
に代入して、
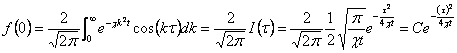
よって、
これより、
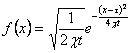
となるので、最終的に、
より、
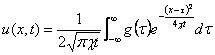
が求める特解の一般形である。